The Dice - Explained
I just popped in here to General Discussion, which I never really visit, and was surprised at the number of dice threads. I've tried to explain this in the past, but nobody seemed to care. I'll try again.
The dice aren't truly random because they are chosen from a set without uniform distribution.
The reason I know the numbers are chosen from a set without uniform distribution is because lack told us so.
A die that is a "good" and "valid" and not "rigged" has the following distribution of numbers on it:
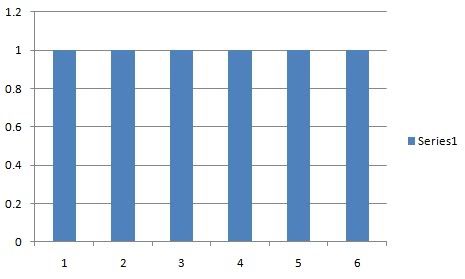
The probability of rolling any one of those numbers is EXACTLY 1/6th.
If you use a random number generator to pick a number out of the above "set", each number has a 1/6th chance of being drawn.
I asked random.org for 10k random numbers between 1 and 6. It gave me the following set:
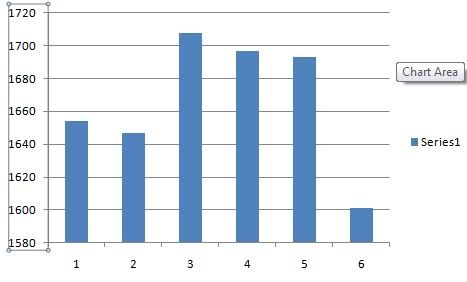
If you use a pseudo random number generator to pick a single number from the above set of numbers (which is what cc does), the odds are NOT 1/6th that each number will be drawn, because the set does not have uniform distribution. During that 1 hour period, before the 50k file is replaced, the odds are higher that you will receive a 3, 4, or 5. Lower that you will receive a 1 or 2, and much lower for a 6.
The next hour, CC will get a new file, and the distribution of the numbers in that set will be different.
Each Hour the "Dice" will be "loaded" differently. Thus, any single number extracted out of it won't be properly random, because the distribution of the set isn't split evenly 1/6th, thus failing to fulfill random.org's definition of a random number, and common sense.
The dice aren't truly random because they are chosen from a set without uniform distribution.
random.org wrote:When discussing single numbers, a random number is one that is drawn from a set of possible values, each of which is equally probable. In statistics, this is called a uniform distribution, because the distribution of probabilities for each number is uniform (i.e., the same) across the range of possible values. For example, a good (unloaded) die has the probability 1/6 of rolling a one, 1/6 of rolling a two and so on. Hence, the probability of each of the six numbers coming up is exactly the same, so we say any roll of our die has a uniform distribution.
The reason I know the numbers are chosen from a set without uniform distribution is because lack told us so.
lackattack wrote:This is how the intensity cubes now work:
* We have a series of 50,000 true random numbers from random.org
* Each time the game engine processes an assault or auto-assault, it select a random spot in the series to read from using a pseudo-random computer function
* Each time the game engine generates a random intensity cube, the next number is read in sequence from the series (e.g. in a 3v1 attack 4 numbers are read sequentially)
* The series of 50,000 true random numbers from random.org is replaced every hour
A die that is a "good" and "valid" and not "rigged" has the following distribution of numbers on it:

The probability of rolling any one of those numbers is EXACTLY 1/6th.
If you use a random number generator to pick a number out of the above "set", each number has a 1/6th chance of being drawn.
I asked random.org for 10k random numbers between 1 and 6. It gave me the following set:

If you use a pseudo random number generator to pick a single number from the above set of numbers (which is what cc does), the odds are NOT 1/6th that each number will be drawn, because the set does not have uniform distribution. During that 1 hour period, before the 50k file is replaced, the odds are higher that you will receive a 3, 4, or 5. Lower that you will receive a 1 or 2, and much lower for a 6.
The next hour, CC will get a new file, and the distribution of the numbers in that set will be different.
Each Hour the "Dice" will be "loaded" differently. Thus, any single number extracted out of it won't be properly random, because the distribution of the set isn't split evenly 1/6th, thus failing to fulfill random.org's definition of a random number, and common sense.