The Dice - Explained

[Army of GOD]

Actually, yes it is, by definition. 1 is between 1 and 6, therefore a random 1 is a random number between 1 and 6.

Then lets play a game.

bedub, from what I've read in this thread, you're wrong.

Guys who are arguing with him: why? There's no point in arguing with a brick wall.

[spiesr]

Here is an idea: Let's just forget about deciding what definition of random we are using and just argue about how well, or unwell, the system simulates the rolling of a fair six sided die.

[PLAYER57832]

When discussing single numbers, a random number is one that is drawn from a set of possible values, each of which is equally probable. In statistics, this is called a uniform distribution, because the distribution of probabilities for each number is uniform (i.e., the same) across the range of possible values. For example, a good (unloaded) die has the probability 1/6 of rolling a one, 1/6 of rolling a two and so on. Hence, the probability of each of the six numbers coming up is exactly the same, so we say any roll of our die has a uniform distribution.

This is the part you got wrong.

See, this applies ONLY TO SINGLE ROLLS. It does not apply to sets of rolls.

First, set aside the fact that dice are not truly rolled randomly. That is there is variation in our hands, in many other things that subtly influence dice. People still rely upon them becuase, for the most part, dice are unpredictable. Also set aside the fact that no computer-generated (or other) random number is really and "truly", in the absolute technical sense, "fully random", becuase its just impossible. Any computer-generated number is far more random and far less predictable than hand-thrown dice.

Now, fast forward to the distribution bit. The uniformity bit only applies to individual rolls, not sequences of rolls. Although the probability for each individual die or roll, for each individual number to appear is roughly even, when you start charting this, you are no longer charting individual rolls. Instead, you are charting the probability for multiple rolls. That is, how often do we roll a 6, then something else. How often do we roll 2 sixes, then something else. If you chart all of these combinations, you will see something like this:

LOTS of single rolls (rolling 6 once, then another number) -- the top of the curve.
Fewer chances of rolling it twice, even fewer chances of getting the same roll.
Eventually, you get something like the chance of rolling 100 rolls in a row is very, very, very, very small.

HOWEVER, note that that probability never reaches 0. So, theoretically, it is just possible for 6 to be legitimately and radomly rolles 1,000,000 times. In practice, the chance is so slim most of us would discount it, but statistically.. that probability exists.

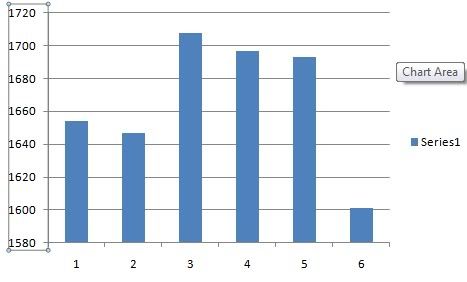
n practice we find that what number actually appears will fall on a bell curve. We call this a standard or normal distribution.

The most "normal" distribution is not that everything would be even, or uniform, but a bell curve.

The reason I know the numbers are chosen from a set without uniform distribution is because lack told us so.

Imagine when you roll, you are rolling a 50,000 sided dice that contains the numbers 1-6. In order for the die to have perfectly uniform distribution, each number would be on the die exactly 8333 1/3rd times. Which obviously can't happen.

Here is, again where you err.

Each die must have an equal chance of appearing. However, for reasons best left to statisticians, the series of rolls in a standard population is a bell curve.
Try it with dice. For a dozen rolls, you will see some pretty skewed graphs, because you will get a few series of 4,5,6...e tc rolls in a row of the same thing. HOWEVER, if you expanded that to something like 2000 rolls, you would find a pretty normal distribution no matter who rolled and no matter how many times you rolled. Not absolutely normal, because you might have a few of the perfectly allowable extreme situations. In fact, you might just happen on an instance of, say 200 rolls in a row of the same thing. However, those occurances would be relatively rare


The biggest problem here IS a failure to understand the difference between probability of getting a particular count in a single roll and the difference between getting a series of rolls. Again, the probability for each individual roll is even. However, the "chance" of getting any particular series of rolls is shown by a bell curve IF its a random selection of a normal, standard population (or just say "if its random, the series will fall on a bell curve)

HOWEVER, there are 2 other issues (3 actually, but the last has nothing to do with the dice) at play here:
First, there are a HUGE number of rolls here. We talk of something being "1 in a million" as if it were exceedingly rare. In fact, there are likely several million rolls every day here in CC! (remember each turn has from 2-5 dice rolled!). This means that what might feel to be "highly improbable" occurances plain happen ... and with what might seem to be heavy regularity just because of theh high numbers of rolls. I mean, your chances of winning the lottery are pretty slim, but people do win!

Second, people don't generally track individual numbers. They track wins and losses. BUT, you can get a lot of wins within a very wide range of rolls. I can roll a 3, a 4 a 5 a 6, then a 2, then a 4.... and win every single roll, if the other player simply rolls (1 or 2), (1,2 or 3), (1,2,3,4), (1,2,3,4,5), (1), (1,2,3). I am not going to bother to list the probabilities for each combination. Just look at how many combinations can get you a win..and definitely NOT because the person rolled "all 6's". So, streaks of individual numbers are absolutely possible in the most random of systems. HOWEVER, you don't really need much of a streak to get a streak of wins.

Thirdly, the actual probability of wins is skewed a bit more because of the natural, rule-based "weighting". Most of you know that the attacker rolls with up to 3, the defender defends with up to 2. That gives the attacker an attack advantage. The defender, however, wins all ties. That gives a defense advantage. Again, I am not going to lay out the statistics (its been done if you are interested). However, this will result in what might seem to be more anomolous streaks which are actually not streaks of rolls, just streaks of wins. That is, the dice are "jumping all around" with their numbers, but the impact seems to be a single streak because you only notice 2 results -- win or lose.

The fourth issue has nothing at all to do with probabilities and statistics. People just plain and simply tend to think they "ought to win" more than lose. It is an inherent, amost "given" bias, perhaps more definite among some players,but slightly there almost always. This means that we tend to remember the time we lose more than the times we win. In turn, this means we have a more negative view of the whole thing. The less mature players take losing the poorest , are also the least likely to truly understand statistics AND are the biggest complainers. However, anyone can be a bit guilty at times.

I know I have found myself wondering at times, but the bottom line is that the dice are random.

[bedub1]

Everything you said I agree with, except the stuff below.

When discussing single numbers, a random number is one that is drawn from a set of possible values, each of which is equally probable. In statistics, this is called a uniform distribution, because the distribution of probabilities for each number is uniform (i.e., the same) across the range of possible values. For example, a good (unloaded) die has the probability 1/6 of rolling a one, 1/6 of rolling a two and so on. Hence, the probability of each of the six numbers coming up is exactly the same, so we say any roll of our die has a uniform distribution.

This is the part you got wrong.

See, this applies ONLY TO SINGLE ROLLS. It does not apply to sets of rolls.

No..I got it right. I quoted random.org. Random.org got it right. The 3rd and 4th words are "single numbers". I'm still only talking about single numbers. In fact, I'm still talking about the very first number selected from the set of 50k numbers by the pseudo random number generator when it is asked for a number.

Imagine when you roll, you are rolling a 50,000 sided dice that contains the numbers 1-6. In order for the die to have perfectly uniform distribution, each number would be on the die exactly 8333 1/3rd times. Which obviously can't happen.

Here is, again where you err.

Again, no, I got it right here. Let me try and explain with graphs.

A die that is a "good" and "valid" and not "rigged" has the following distribution of numbers on it:


The probability of rolling any one of those numbers is EXACTLY 1/6th.
If you use a random number generator to pick a number out of the above "set", each number has a 1/6th chance of being drawn.

I asked random.org for 10k random numbers between 1 and 6. It gave me the following set:

If you use a pseudo random number generator to pick a single number from the above set of numbers (which is what cc does), the odds are NOT 1/6th that each number will be drawn, because the set does not have uniform distribution. During that 1 hour period, before the 50k file is replaced, the odds are higher that you will receive a 3, 4, or 5. Lower that you will receive a 1 or 2, and much lower for a 6.

The next hour, CC will get a new file, and the distribution of the numbers in that set will be different.

Each Hour the "Dice" will be "loaded" differently. Thus, any single number extracted out of it won't be properly random, because the distribution of the set isn't split evenly 1/6th, thus failing to fulfill random.org's definition of a random number, and common sense.

I don't see how I can explain this any simpler. Does this help?

[Metsfanmax]

If you use a pseudo random number generator to pick a single number from the above set of numbers (which is what cc does), the odds are NOT 1/6th that each number will be drawn, because the set does not have uniform distribution. During that 1 hour period, before the 50k file is replaced, the odds are higher that you will receive a 3, 4, or 5. Lower that you will receive a 1 or 2, and much lower for a 6.

The next hour, CC will get a new file, and the distribution of the numbers in that set will be different.

Each Hour the "Dice" will be "loaded" differently. Thus, any single number extracted out of it won't be properly random, because the distribution of the set isn't split evenly 1/6th, thus failing to fulfill random.org's definition of a random number, and common sense.

I don't see how I can explain this any simpler. Does this help?

You still seem to not understand that is the nature of random processes. Uniform distributions are unlikely for small samples. This is the very nature of random. Consider a perfectly fair coin, or other process which we know to be truly random (say, radioactivity) and can be mapped into a binary result. The probability that after 50,000 flips the number of heads would be exactly 25,000, is less than 0.5%. If we followed your logic, we'd conclude that the random process was, in fact, not random.

Anyway, a process that guaranteed a uniform distribution for an arbitrary sample size would not be random.

[bedub1]

If you use a pseudo random number generator to pick a single number from the above set of numbers (which is what cc does), the odds are NOT 1/6th that each number will be drawn, because the set does not have uniform distribution. During that 1 hour period, before the 50k file is replaced, the odds are higher that you will receive a 3, 4, or 5. Lower that you will receive a 1 or 2, and much lower for a 6.

The next hour, CC will get a new file, and the distribution of the numbers in that set will be different.

Each Hour the "Dice" will be "loaded" differently. Thus, any single number extracted out of it won't be properly random, because the distribution of the set isn't split evenly 1/6th, thus failing to fulfill random.org's definition of a random number, and common sense.

I don't see how I can explain this any simpler. Does this help?

You still seem to not understand that is the nature of random processes. Uniform distributions are unlikely for small samples. This is the very nature of random. Consider a perfectly fair coin, or other process which we know to be truly random (say, radioactivity) and can be mapped into a binary result. The probability that after 50,000 flips the number of heads would be exactly 25,000, is less than 0.5%. If we followed your logic, we'd conclude that the random process was, in fact, not random.

Anyway, a process that guaranteed a uniform distribution for an arbitrary sample size would not be random.

No I completely get that. But in order to get a random number you have to pick from something with a uniform distribution, not from something with a random distribution.

[Metsfanmax]

If you use a pseudo random number generator to pick a single number from the above set of numbers (which is what cc does), the odds are NOT 1/6th that each number will be drawn, because the set does not have uniform distribution. During that 1 hour period, before the 50k file is replaced, the odds are higher that you will receive a 3, 4, or 5. Lower that you will receive a 1 or 2, and much lower for a 6.

The next hour, CC will get a new file, and the distribution of the numbers in that set will be different.

Each Hour the "Dice" will be "loaded" differently. Thus, any single number extracted out of it won't be properly random, because the distribution of the set isn't split evenly 1/6th, thus failing to fulfill random.org's definition of a random number, and common sense.

I don't see how I can explain this any simpler. Does this help?

You still seem to not understand that is the nature of random processes. Uniform distributions are unlikely for small samples. This is the very nature of random. Consider a perfectly fair coin, or other process which we know to be truly random (say, radioactivity) and can be mapped into a binary result. The probability that after 50,000 flips the number of heads would be exactly 25,000, is less than 0.5%. If we followed your logic, we'd conclude that the random process was, in fact, not random.

Anyway, a process that guaranteed a uniform distribution for an arbitrary sample size would not be random.

No I completely get that. But in order to get a random number you have to pick from something with a uniform distribution, not from something with a random distribution.

I don't think you're understanding the consequences of the argument, so let's do a thought experiment. Let's say that instead of pseudo-randomly picking a spot on the list to start, we just got a list of 1 trillion numbers from random.org and read it sequentially, moving up a few spots after every roll. Would that process be fair and random?

[bedub1]

If you use a pseudo random number generator to pick a single number from the above set of numbers (which is what cc does), the odds are NOT 1/6th that each number will be drawn, because the set does not have uniform distribution. During that 1 hour period, before the 50k file is replaced, the odds are higher that you will receive a 3, 4, or 5. Lower that you will receive a 1 or 2, and much lower for a 6.

The next hour, CC will get a new file, and the distribution of the numbers in that set will be different.

Each Hour the "Dice" will be "loaded" differently. Thus, any single number extracted out of it won't be properly random, because the distribution of the set isn't split evenly 1/6th, thus failing to fulfill random.org's definition of a random number, and common sense.

I don't see how I can explain this any simpler. Does this help?

You still seem to not understand that is the nature of random processes. Uniform distributions are unlikely for small samples. This is the very nature of random. Consider a perfectly fair coin, or other process which we know to be truly random (say, radioactivity) and can be mapped into a binary result. The probability that after 50,000 flips the number of heads would be exactly 25,000, is less than 0.5%. If we followed your logic, we'd conclude that the random process was, in fact, not random.

Anyway, a process that guaranteed a uniform distribution for an arbitrary sample size would not be random.

No I completely get that. But in order to get a random number you have to pick from something with a uniform distribution, not from something with a random distribution.

I don't think you're understanding the consequences of the argument, so let's do a thought experiment. Let's say that instead of pseudo-randomly picking a spot on the list to start, we just got a list of 1 trillion numbers from random.org and read it sequentially, moving up a few spots after every roll. Would that process be fair and random?

yes, that's how it's supposed to be done. but you don't move up a few spots after every roll. just read the entire file sequentially, discard it, and move on.

[Metsfanmax]

yes, that's how it's supposed to be done. but you don't move up a few spots after every roll. just read the entire file sequentially, discard it, and move on.

Okay, now let's say we count up the distribution of numbers in that file and it turns out that the number of 6's is not 16.6666...% but is actually 17%, and the number of 3's is 16.3333...%. Would you still assert that the sequential reading of the file is a fair and random process?

[bedub1]

yes, that's how it's supposed to be done. but you don't move up a few spots after every roll. just read the entire file sequentially, discard it, and move on.

Okay, now let's say we count up the distribution of numbers in that file and it turns out that the number of 6's is not 16.6666...% but is actually 17%, and the number of 3's is 16.3333...%. Would you still assert that the sequential reading of the file is a fair and random process?

absolutely. thats randomness. If it had a perfect distribution i'd wonder about it. if you get enough "sets" eventually it will happen(thats the randomness of randomness)...but I'm sure not that often...anybody want to calculate the probability? (good luck with that one...better off plotting it's history) (rolling 6 dice, only approximately 1.54% of the time will they all be different(perfect distribution....what happens when you roll 60k?)

But if you start randomly picking from a list of random numbers you run into the problems that I've described. The set of true random numbers is now nothing more than a set of numbers, and you are dependent upon your pseudo random number generator, which sucks, and then is picking from a set of numbers without perfect distribution, which sucks even more. Is this making sense?

Do you guys agree with this: A number in and of itself isn't random, it's how you come about choosing it that determines if it's random or not.

[Metsfanmax]

yes, that's how it's supposed to be done. but you don't move up a few spots after every roll. just read the entire file sequentially, discard it, and move on.

Okay, now let's say we count up the distribution of numbers in that file and it turns out that the number of 6's is not 16.6666...% but is actually 17%, and the number of 3's is 16.3333...%. Would you still assert that the sequential reading of the file is a fair and random process?

absolutely. thats randomness. If it had a perfect distribution i'd wonder about it. if you get enough "sets" eventually it will happen(thats the randomness of randomness)...but I'm sure not that often...anybody want to calculate the probability? (good luck with that one...better off plotting it's history)

But if you start randomly picking from a list of random numbers you run into the problems that I've described. The set of true random numbers is now nothing more than a set of numbers, and you are dependent upon your pseudo random number generator, which sucks, and then is picking from a set of numbers without perfect distribution, which sucks even more. Is this making sense?

Okay, I can now make my point properly. You've agreed that if the set we read from linearly is non-uniform, the process is still fair and random. The underlying reason is that you know that the list is simply a proxy for calling the random number generator 1 trillion times; the result of reading the first number in the list at 8 PM is equivalent to having submitted a request to random.org at 8 PM for a number. Similarly, when there have been a number of additional rolls, the result of reading the 2000th number in the list at 8:05 PM is equivalent to having submitted a request to random.org at 8:05 PM for a number. Every spot on the list gives you a fair and random chance to get a result from 1-6, when the numbers are read linearly. So the question is, when the spot on the list is chosen pseudo-randomly, why does this property of the numbers suddenly change?

[bedub1]

So the question is, when the spot on the list is chosen pseudo-randomly, why does this property of the numbers suddenly change?

It's not the property of the numbers that changes, it's the way the number is chosen that has changed.

Q2.3: Should the tables of generated numbers be read across or down?

For any form that allows the numbers to be formatted in multiple columns, the numbers are generated on a per-row basis, not per-column. Hence, if you want to read them in the order they were generated, you should read them across. Since they're random numbers, it doesn't really matter whether you do it one way or the other, but you should pick one of the two ways and read that way consistently.

We do not read the numbers consistently, which is what we should be doing. What we do is read them "randomly" which corrupts the entire process. We are no longer reading random numbers properly. We are now running a pseudo-random number generator on a set of random numbers, which doesn't result in random numbers, but in biased numbers.

[Metsfanmax]

So the question is, when the spot on the list is chosen pseudo-randomly, why does this property of the numbers suddenly change?

It's not the property of the numbers that changes, it's the way the number is chosen that has changed.

Q2.3: Should the tables of generated numbers be read across or down?

For any form that allows the numbers to be formatted in multiple columns, the numbers are generated on a per-row basis, not per-column. Hence, if you want to read them in the order they were generated, you should read them across. Since they're random numbers, it doesn't really matter whether you do it one way or the other, but you should pick one of the two ways and read that way consistently.

We do not read the numbers consistently, which is what we should be doing. What we do is read them "randomly" which corrupts the entire process. We are no longer reading random numbers properly. We are now running a pseudo-random number generator on a set of random numbers, which doesn't result in random numbers, but in biased numbers.

This logic simply doesn't follow. You must agree that in the example I cited, a player is more likely to get a 6 than a 3 even if the file is read linearly, due to the fact that there are more 6's than 3's. In fact, the increased probability of getting a 6 compared to 3 is exactly the same as in the case where the starting point is chosen pseudo-randomly. The argument, therefore, that the linear case is fair and random and the PRNG case is not, leads to a logical contradiction, which means you must abandon your hypothesis.

[bedub1]

This logic simply doesn't follow. You must agree that in the example I cited, a player is more likely to get a 6 than a 3 even if the file is read linearly, due to the fact that there are more 6's than 3's.

Of course. But the file is read once, and sequentially. Each location in the file is read once and only once.

In fact, the increased probability of getting a 6 compared to 3 is exactly the same as in the case where the starting point is chosen pseudo-randomly.

Not at all. Using a Pseudo random generator to pick a spot to read, each spot can be read MORE THAN ONCE.

Think of this. If you create a file of the numbers 1-6, 60k numbers long, and it ends up with a distribution of numbers like this:
and then read it randomly to make another file 60k numbers long, the 2nd file will have a higher distribution of the numbers that was in the original file more than the others. If you do this again to create a 3rd file, the distortion will get larger. If you do it an infinite number of times, eventually the file will have only 1 number in it, repeated 60k times. Can someone create a model to test this theory?

[Metsfanmax]

Think of this. If you create a file of the numbers 1-6, 60k numbers long, and it ends up with a distribution of numbers like this:
and then read it randomly to make another file 60k numbers long, the 2nd file will have a higher distribution of the numbers that was in the original file more than the others. If you do this again to create a 3rd file, the distortion will get larger. If you do it an infinite number of times, eventually the file will have only 1 number in it, repeated 60k times. Can someone create a model to test this theory?

Incorrect. If the method for picking the numbers is truly random, or good enough to be indistinguishable from random (which modern PRNGs are) then the second file will, on average, have the same distribution as the first.

[bedub1]

The first set is perfect distribution. 1 of each number on the side of a die. The second set I graphed the results for you in my previous posts. You can see it doesn't have a perfect distribution, like the first file. I just ran my own little test using random.org. Here are the results.



I rolled 6 die. I got the number in A1-A6. I rolled 6 die, and got the numbers in B8-B13. I used those numbers to pick the spot to read from the previous "results"(A1-A6) and ended up with the numbers in B1-B6. I rolled 6 die again, and got the numbers in C8-C13. I used those numbers to pick the spot to read from the previous "results (B1-B6) and ended up with the numbers in C1-C6. I did it "S" number of times until I ended up with nothing but a bunch of 3's.

I believe my test has just proved my theory. I'm not going to do it again cause it was a pain.

[Metsfanmax]

The first set is perfect distribution. 1 of each number on the side of a die. The second set I graphed the results for you in my previous posts. You can see it doesn't have a perfect distribution, like the first file. I just ran my own little test using random.org. Here are the results.



I rolled 6 die. I got the number in A1-A6. I rolled 6 die, and got the numbers in B8-B13. I used those numbers to pick the spot to read from the previous "results"(A1-A6) and ended up with the numbers in B1-B6. I rolled 6 die again, and got the numbers in C8-C13. I used those numbers to pick the spot to read from the previous "results (B1-B6) and ended up with the numbers in C1-C6. I did it "S" number of times until I ended up with nothing but a bunch of 3's.

I believe my test has just proved my theory. I'm not going to do it again cause it was a pain.

No. Your sample size is tiny and you only ran one sample. I did it better. Here's the MATLAB code I used:

clear
clc

initNums(1:9500) = 1;
initNums(9501:18500) = 2;
initNums(18501:28000) = 3;
initNums(28001:38500) = 4;
initNums(38501:50500) = 5;
initNums(50501:60000) = 6;

newNums = zeros(1,60000);

for j = 1:100
newNums = zeros(1,60000);
for i = 1:60000
randNum = rand(1,1);
selectedSpot = ceil(60000*randNum);
newNums(i) = initNums(selectedSpot);
end
initNums = newNums;
end

result = histc(newNums,[1 2 3 4 5 6]);

bar(result)

This code generates a flawed distribution of length 60,000, and selects a random spot on the list to read 60,000 times. It then uses this new matrix as the input, and repeats the process 99 more times.

Here's the initial distribution:



Here's the final distribution:



I did it again:



And again:



And again:

[Metsfanmax]

Just because I can, I ran the same code but with 1000 steps instead of 100.

Initial distribution:



Result 1:



Result 2:



Result 3:



It should be evident that a flawed distribution does not guarantee a distribution more flawed in the same direction after this trial, as your theory seems to indicate. If you don't believe it, run the code yourself. If you don't have access to MATLAB (or an open source variant such as Octave), I can help explain how to port the code to C/C++ or FORTRAN.

[bedub1]

It should be evident that a flawed distribution does not guarantee a distribution more flawed in the same direction after this trial, as your theory seems to indicate. If you don't believe it, run the code yourself. If you don't have access to MATLAB (or an open source variant such as Octave), I can help explain how to port the code to C/C++ or FORTRAN.

Thanks for running those. I do believe you. You provided proof. It should have been obvious to me when my column C was 5 of 1 and one of the other, yet the single ended up winning. But I have still have questions. Can you run more simulations for me?

Run 2 sets, 1 with a non-uniform distribution, one with a perfectly uniform distribution, but run it 10 times, graph, 100 times, graph, 1000 times, graph, 10,000 times, graph. Of the same iteration. I feel that as the number of runs approaches infinity, that the distribution will stop being uniform, and will start to oscillate out of control. The reason I think this is thus:

In your 100 run, you start with a distribution that is "basically" even...with a single on 20% higher than the others. (10,000 vs 12,000) After your runs, it's 8000 vs 12,000,

In your 1000 run, you start with a distribution that is "basically" even...with a single one 50% higher than the others(10,000 vs 15,000). After your runs, its 4 times larger.

Plus this is the basis for my argument. That running a random number generator on the results of another random number generator is a bad idea, because it doesn't produce good results. You can only run a random number generator on a set with uniform distribution.

[Metsfanmax]

In your 100 run, you start with a distribution that is "basically" even...with a single on 20% higher than the others. (10,000 vs 12,000) After your runs, it's 8000 vs 12,000,

In your 1000 run, you start with a distribution that is "basically" even...with a single one 50% higher than the others(10,000 vs 15,000). After your runs, its 4 times larger.

Plus this is the basis for my argument. That running a random number generator on the results of another random number generator is a bad idea, because it doesn't produce good results. You can only run a random number generator on a set with uniform distribution.

Actually I think you might have misinterpreted my first post. Each of the four graphs after the first one is the result of doing 100 iterations on the initial distribution. In the last simulation it is indeed the case that the number which started higher initially ended up higher. But in the other three cases it is definitely different. My point was that if you did enough of these 100-iteration runs and averaged them, you would get something close to the initial distribution (proving that using a PRNG on a given data set does not exaggerate a non-uniform distribution). I only ran four of these, which is not nearly sufficient.

Run 2 sets, 1 with a non-uniform distribution, one with a perfectly uniform distribution, but run it 10 times, graph, 100 times, graph, 1000 times, graph, 10,000 times, graph. Of the same iteration. I feel that as the number of runs approaches infinity, that the distribution will stop being uniform, and will start to oscillate out of control.

So, to more justifiably prove my point, what I will do is leave a large set of simulations on overnight. I will do two sets. In one, I will run 25,000 simulations of a 100-iteration run on an initially non-uniform distribution of 60,000 numbers with 5000 extra 6s and 5000 fewer 3s (the rest being equal at 10,000 each). I will report the percentage of simulations which have more 6s than were started with (15,000). In the other set, I will run 25,000 simulations on an initially uniform distribution, and report that same percentage (number of simulations with more than 10,000 - in this case - 6s). If your theory is correct, we would expect the result of the second test to be about 50%, and the result of the first test to be significantly above 50%. If my theory is correct, we would expect both tests to report about 50%. I won't be providing nifty graphs this time but I don't really feel like generating and saving 25,000 graphs ;P

[bedub1]

Did you get a chance to run those?

[Metsfanmax]

Did you get a chance to run those?

I did start the simulations that evening, but I realized after how stupid I was being. Each simulation takes about a minute on my laptop, so I was looking about a month of calculations. I'll cut down a bit on the number of simulations and run it in parallel on my desktop when I get a chance - I'll post here when I've done that.

[Dukasaur]

A "uniform distribution" is a purely hypothetical beast, something we study in algebra class but will never encounter in real life. Even in intergalactic space, particles are not uniformly distributed -- there are swirls of greater and lesser density. So, the question here is perhaps: what do you expect from your dice? Do you expect them to behave "fairly" like the hypothetical construct, or do you expect them to behave in accordance with the unfairness that is inherent in our chaotically non-uniform universe?

[Metsfanmax]

123456

Oh look, a wild uniform distribution appears

[natty dread]

123456

Oh look, a wild uniform distribution appears

Shoot it before it gets away!